Effects of
radiative emission and absorption
on the propagation and extinction of premixed gas flames
Yiguang Ju and Goro Masuya
Department of Aeronautics and Space Engineering
Tohoku University, Aoba-ku, Sendai 980, Japan
and
Paul D. Ronney
Department of Aerospace and Mechanical Engineering
University of Southern California, Los Angeles, CA 90089-1453 USA
Abstract
Premixed gas flames in mixtures of CH4, O2, N2 and CO2 were studied numerically using detailed chemical and radiative emission-absorption models to establish the conditions for which radiatively-induced extinction limits may exist independent of the system dimensions. It was found that reabsorption of emitted radiation led to substantially higher burning velocities and wider extinction limits than calculations using optically-thin radiation models, particularly when CO2, a strong absorber, is present in the unburned gas. Two heat loss mechanisms that lead to flammability limits even with reabsorption were identified. One is that for dry hydrocarbon-air mixtures, because of the differences in the absorption spectra of H2O and CO2, most of the radiation from product H2O that is emitted in the upstream direction cannot be absorbed by the reactants. The second is that the emission spectrum of CO2 is broader at flame temperatures than ambient temperature, thus some radiation emitted near the flame front cannot be absorbed by the reactants even when they are seeded with CO2. Via both mechanisms some net upstream heat loss due to radiation will always occur, leading to extinction of sufficiently weak mixtures. Downstream loss has practically no influence. Comparison to experiment demonstrates the importance of reabsorption in CO2-diluted mixtures. It is concluded that fundamental flammability limits can exist due to radiative heat loss, but these limits are strongly dependent on the emission-absorption spectra of the reactant and product gases and their temperature dependence, and cannot be predicted using gray-gas or optically-thin model parameters. Applications to practical flames at high pressure, in large combustion chambers and with exhaust-gas or flue-gas recirculation are discussed.
Published in the Proceedings of the Twenty-Seventh International Symposium on Combustion, Combustion Institute, Pittsburgh, 1998, pp. 2619-2626.
Introduction
Flammability limit studies are important for assessment of fire safety in many environments and determining the operation limits of combustion devices. Despite many years of study, the mechanisms of flammability limits of premixed gas flames are still not well understood. In particular, it has not been established whether "fundamental" limits exist independent of apparatus size and geometry. Many loss mechanisms cause apparatus-dependent extinction limits including flame stretch [1,2], buoyant convection [3,4] and heat losses to cold walls [5-7]. When these losses are eliminated by employing large combustion vessels at microgravity, heat loss via gaseous radiation is probably the dominant extinction mechanism [8-11].
Nevertheless, it is unclear whether radiative loss causes fundamental limits because emitted radiation can be reabsorbed, a factor not considered by the theories [6,7] and computations [10,11]. Whether reabsorption is important is usually assessed by comparing the system dimension to the burned-gas Planck mean absorption length (LP), defined as the mean monochromatic absorption coefficient (k) weighted by the Planck function:
![]() (1),
(1),
where h, c, w, k and T denote Planck’s constant, light speed, wavenumber, Boltzman’s constant and temperature, respectively. In the experiments [8,9], the optical thickness tºX/LP, where X is an apparatus dimension, was generally small (with exceptions noted later), consequently optically-thin conditions (no reabsorption) applied. Theoretical studies of premixed-gas flames seeded with inert particles [12] predict that with reabsorption, net heat losses decrease, burning velocities (SL) increase and the flammability limit equivalence ratio (Fo) decreases compared to values without reabsorption. Corresponding microgravity experiments in particle-laden methane-air mixtures [13] support these predictions. Gaseous flame behavior should be different from particle-laden flames because gases emit and absorb in spectral bands whereas particles exhibit approximately gray-gas behavior. No computational studies of gaseous flames with detailed radiative emission/absorption models have been performed to test their effects on SL and Fo. Consequently, our goal is to model premixed-gas flame propagation with detailed radiative emission/absorption effects and compare results to experiments and theoretical predictions.
In addition to microgravity studies, modeling of premixed-gas flames with reabsorption is relevant to combustion at high pressures and in large furnaces because frequently t>1. For example, at 40 atm, a typical pressure for premixed-charge IC engines, tŠ1 for cylinders of radius 4 cm. Similarly, t>1 in atmospheric-pressure furnaces larger than 1.6 m. Moreover, significant amounts of absorbing CO2 and H2O are present in the unburned mixtures of combustion devices employing exhaust-gas or flue-gas recirculation.
Numerical model
The energy and chemical species conservation equations for steady planar premixed-gas flames were solved using a CHEMKIN-based code [14] with arclength continuation [15,16]. This code was employed previously to model optically-thin radiating counterflow flames [16]. For this study, radiative transport including both emission and absorption was computed using the statistical narrow-band model with exponential-tailed inverse line strength distribution [17]. The radiative transfer equations were solved for wavenumbers between 150 and 9300 cm-1 with 25 cm-1 resolution using the S6 discrete ordinate method. Radiation parameters for CO2, H2O and CO were taken from [18]. CH4 radiation was not included because the necessary spectral data were not available, but CH4 radiation is minimal even for optically-thin conditions [11]. Further details, including accuracy considerations, are presented elsewhere [19]. Methane oxidation was modeled using a 18-species, 58-step chemical mechanism [14]. The spatial position (x)=0 was defined as the location where T=325K for radiation-free flames. Except where noted, the upstream and downstream boundary locations were x=-L1=-30 cm and x=+L2=+400 cm, respectively. Upstream boundary conditions were ambient temperature (300K) and composition with inflow velocity SL and downstream boundary conditions were zero-gradient. Ambient-temperature blackbody walls were assumed at both boundaries.
Mixtures of CH4 + {0.21O2+(0.79-g)N2+gCO2} were examined, with g varied to assess reabsorption effects by substituting emitting/absorbing CO2 for radiatively-inactive N2. Ambient H2O was not considered because experiments at standard conditions allow at most 3% H2O without condensation.
Results
Figure 1 shows typical computed results. For optically-thin conditions, the volumetric radiative loss (QR)=4s(T4-To4)/LP, where s is the Stefan-Boltzman constant and To the ambient temperature, is always positive (upper plot). With reabsorption QR is negative at x<0 since some radiation emitted at high T (x>0) is reabsorbed at lower T (x<0). This decreases the net loss and preheats the unburned mixture so that, consistent with theory [12], the peak temperature (T*) exceeds adiabatic (Tad) (upper plot). With optically-thin radiative loss, T decays downstream to To (lower plot). With reabsorption T still decays downstream (but on a much longer scale), thus some net loss still occurs. All flames exhibit conventional convective-diffusive zones of thickness dºa/SLš0.1 cm, where a is the temperature-averaged thermal diffusivity. The reabsorbing flame additionally exhibits a much longer upstream convective-radiative zone (lower plot) whose length is comparable to LP (š19 cm).
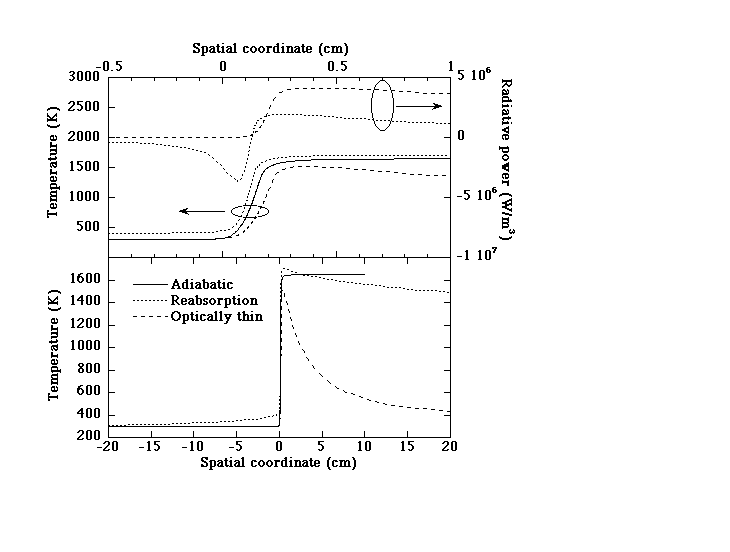
Figure 1. Example of model predictions for F=0.70, g=0.30 (near the lean flammability limit for optically-thin flames) for adiabatic, optically-thin and reabsorbing flames. The corresponding burning velocities are 7.9, 5.9 and 12.7 cm/s, respectively. The optical thickness tºL1/LP is 2.39. Upper plot: temperature (T) and radiative power (QR), -0.5<x<1.0 cm; lower plot: temperature only, -20<x<20 cm.
Figure 2a shows that reabsorption effects in CH4-air mixtures (g=0) are minor since Fo is reduced only 3.8% and even with reabsorption SL is always less than the adiabatic burning velocity (SL,ad). However, SL,lim is reduced by 25% and SL,ad for the limit mixture decreases similarly (26%). For both optically-thin and reabsorption models, SL,lim/SL,ad is close to the theoretical prediction e-1/2 [6,7]. A simple picture emerges from these results. Radiation from hot H2O and CO2 can escape only if is emitted upstream because downstream radiation will be reabsorbed by other H2O and CO2 molecules. Thus, reabsorption approximately halves the net heat loss. Theory for optically-thin flames [6,7] predicts SL,lim~QR1/2, thus if QR were halved SL,lim should decrease 29%. Consequently, the classical quenching mechanism approximately applies in this case.
|
(a) Lean CH4-air mixtures |
|
(b) Lean CH4-(0.21O2+0.49N2+0.30CO2) mixtures (g=0.30) |
Figure 2. Predicted burning velocities and peak flame temperatures under adiabatic conditions, with optically-thin radiative losses, and with a radiative model including reabsorption effects. In this and subsequent figures, the turning-point limit is shown but for clarity the unstable lower solution branch is omitted.
Flame characteristics are quite different with g=0.30 (Fig. 2b). As with g=0, for optically-thin radiation SL and T* are lower than adiabatic values, but with CO2 substitution, because of reabsorption these quantities are significantly higher than adiabatic values. The effect on Fo is substantial (0.682 for optically-thin conditions vs. 0.442 with reabsorption). Nevertheless, flammability limits still exist.
|
(a) Absorption spectra k(w) for pure CO2 and H2O at 1300K and 300K |
|
| (b) Radiative heat flux at cold (upstream) boundary for F=0.50, g=0.30 (tš2.39) with reabsorption effects included. Note that the units on the vertical axis are Watts/m2 per m-1 = Watts/m, i.e., the radiant flux per unit wavenumber. Also shown is ¹Ib, where Ib is the Planck function for a blackbody at T* for this flame, i.e., the maximum possible flux. |
Figure 3. Radiative properties of combustion gases as a function of wave number (w)
Figures 3a-b elucidate two mechanisms that cause net heat loss and thus flammability limits even with reabsorption, designated (I) and (II). Mechanism (I) is that k(w) is very different for H2O and CO2 (Fig. 3a); since H2O is absent from the unburned gas, most H2O radiation emitted upstream cannot be reabsorbed. Mechanism (II) is that k(w) for CO2 is broader at T* than To (Fig. 3a), thus some CO2 radiation emitted upstream from temperatures near T* cannot be reabsorbed farther upstream where TšTo. Mechanism (II) can also occur for H2O but not for the dry reactants studied here. Both mechanisms apply for arbitrarily large domains. The manifestation of these mechanisms is seen in the spectrally-resolved radiative flux at the upstream boundary (x=-L1) (Fig. 3b). The spectrum for CO2+H2O+CO is similar to the CO2+H2O spectra at 1300K (Fig. 3a) less the CO2 spectrum at 300K, indicating that losses arise mainly from the differences between the burned-gas emission and unburned-gas absorption. H2O emission comprises most of the loss (mechanism (I)), but some occurs from CO2 emission (mechanism (II)).
These observations show that fundamental flammability limits due to radiative losses will exist in gaseous flames no matter how large the domain or what absorbing gases are present, because some radiation emitted from the high-temperature region cannot be reabsorbed by the unburned gases (mechanism II). These limits depend upon the temperature effects on the absorption spectrum and cannot be predicted via simple mean absorption coefficients as optically-thin limits can. Of course, if sufficient quantities of inert particles, soot or other quasi-graybody absorbers are present, complete reabsorption could occur.
Loss at the downstream boundary (x=L2) is much less important for several reasons. A disappearing reactant (e.g. CH4) can produce some loss at x=L2 via mechanism I, but CH4 radiation was not considered and the loss would be much less than the upstream H2O and CO2 loss because CH4 disappears near x=0 just as T rises to values where significant radiation could be emitted. Downstream loss via mechanism (II) can occur because of the downstream temperature gradient, but the gradient and total decrease in T are much less than the corresponding upstream values, leading to much lower downstream loss. A third mechanism of radiative loss occurs at the downstream boundary because of the blackbody wall with T=To, but due to reabsorption its influence is confined to the adjacent region of thickness LP (š18 cm). Thus, T* and SL are unaffected, as was verified by changing L2 from 400 to 100 cm.
Losses via mechanisms I or II can occur only for wavenumbers where k(w) is nonzero on one side of the flame but changes to zero over a length smaller than the scale{k(w)}-1 over which reabsorption occurs. Changes occur on the scale d for temperature and Di/SL for species i, where Di is the diffusion coefficient. Since the Lewis numbers a/Di are close to unity, d is an appropriate scale for both species and temperature changes. Hence, these criteria become
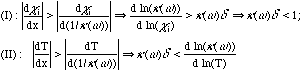 (2)
(2)
where ci is the mole fraction of species i and the fact k~ci has been used. Figure 3b shows evidence of these criteria. The loss due to H2O mimics k(w) except where k(w) is very large and reabsorption can occur within the convective-diffusive zone where cH2O changes rapidly. For CO2 practically no loss occurs where k(w) is large at both 300K and 1300K (Fig. 3a), but substantial loss occurs for w on the "wings" of these peaks where dk/dT is large.
The convective-radiative zone at x<0 has a characteristic thickness LP>>d, thus L1 can influence reabsorbing flames drastically. Figure 4 shows that Fo decreases as L1 increases since more reabsorption (thus lower net QR) occurs with larger L1. Since SL,lim~QR1/2, SL,lim also decreases. Significant reabsorption effects occur even for L1=1 cm (t=0.054) because CO2 has absorption bands with k(w) up to 4000 m-1atm-1 (40 cm-1atm-1) (Fig. 3a). For the limit conditions at L1=1 cm, cH2O=0.19, thus significant absorption occurs on the scale (0.190*40 cm-1)-1=0.13 cm. This estimated minimum reabsorption scale is also seen in Fig. 1, which shows the negative (absorption) portion of QR decaying on a similar scale. Still, L1>100 cm (t>5.4) is required to obtain domain-independent results because the band "wings" have much smaller k(w) and thus longer absorption lengths. Consequently, t provides only limited insight on flame properties with reabsorption.
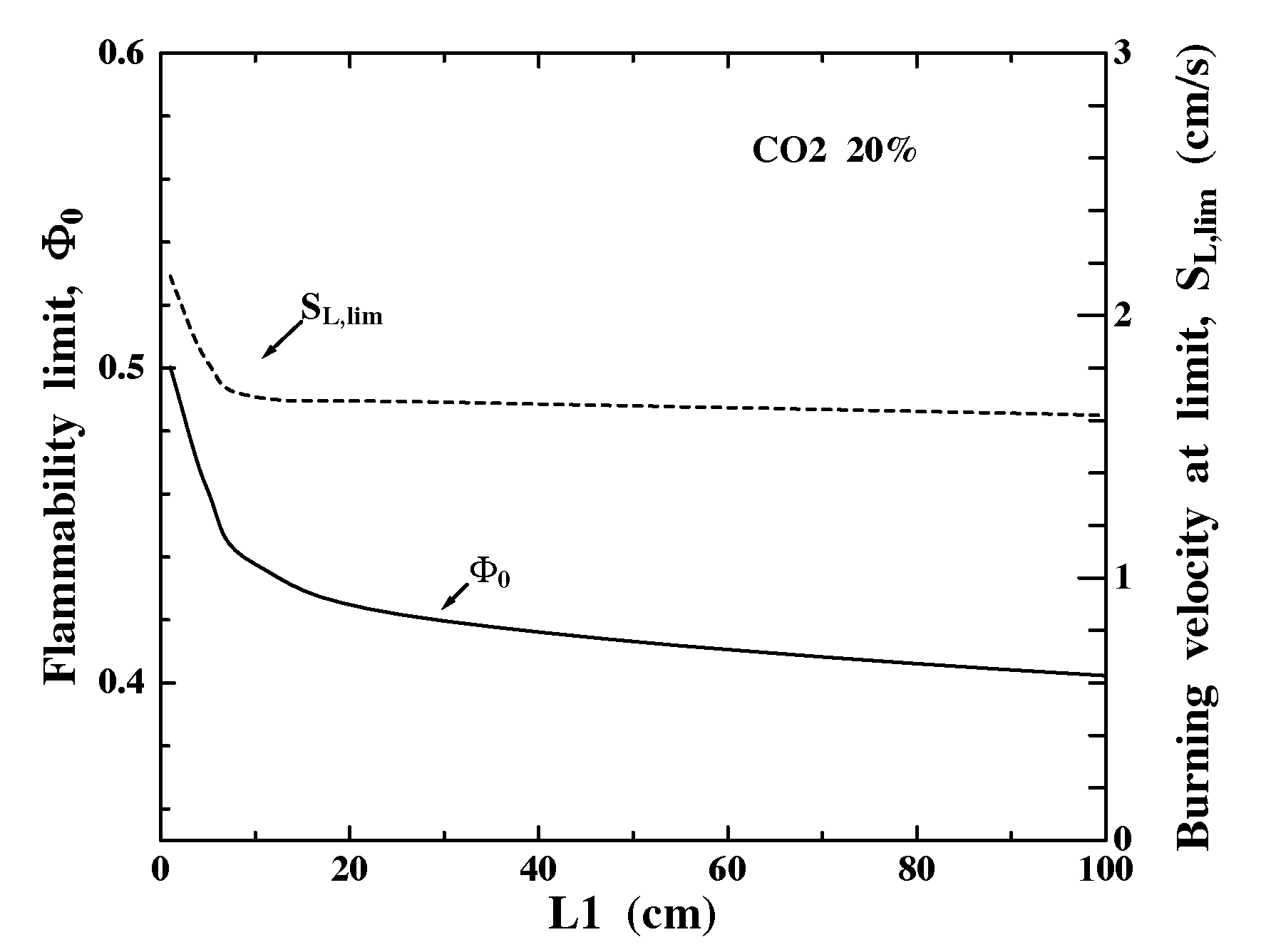
Figure 4. Effect of upstream domain length (L1) on flammability limit properties: equivalence ratio (Fo) and burning velocity (SL,lim) for g=0.20. The corresponding flammability limit for optically-thin conditions is Fo=0.62.
Accurate determination of QR for small k is difficult because for each 25 cm-1 spectral window k(w) characterizes the sum of many individual absorption lines of widely varying strengths. For some individual lines but not others, absorption coefficients are factors of 1030 higher at 1300K than at 300K. Some lines overlap in w-space while others are separated by transparent gaps that are required for net loss via mechanisms I or II to occur. Clearly a single k(w,T) for each spectral window cannot capture all relevant details. Thus, while the reabsorption effects on flame characteristics proposed here are believed valid, quantitative predictions will vary slightly depending on spectral resolution, line-shape model, etc., especially for large L1.
Figure 5 shows that for all radiation models, substituting CO2 for N2 has only minor effects on SL in F=1.0 mixtures, except when g is high enough to reduce Tad and thus SL,ad appreciably. In contrast, only 1% CO2 substitution nearly doubles SL for reabsorbing F=0.5 mixtures. There are two reasons CO2 reabsorption effects are stronger at F=0.5. First, F=0.5 mixtures are much closer to the radiative extinction limit (note for optically-thin F=0.5 mixtures very small amounts of CO2 cause extinguishment due to increased QR) and thus benefit more from the reduction in QR via reabsorption. Second, F=0.5 mixtures have much higher Boltzman numbers (B), which is a scaled ratio of blackbody emissive power at Tad to total heat release rate and thus measures the potential for radiative preheating to increase SL. For non-scattering media [12]
![]() (3)
(3)
where b, E , R, ro and CP represent non-dimensional activation energy, overall activation energy, gas constant, ambient density and specific heat, respectively. Values of B for g=0 mixtures are about 11.3 and 127 for F=1.0 and 0.50, respectively, thus reabsorption can increase SL much more in F=0.5 mixtures.
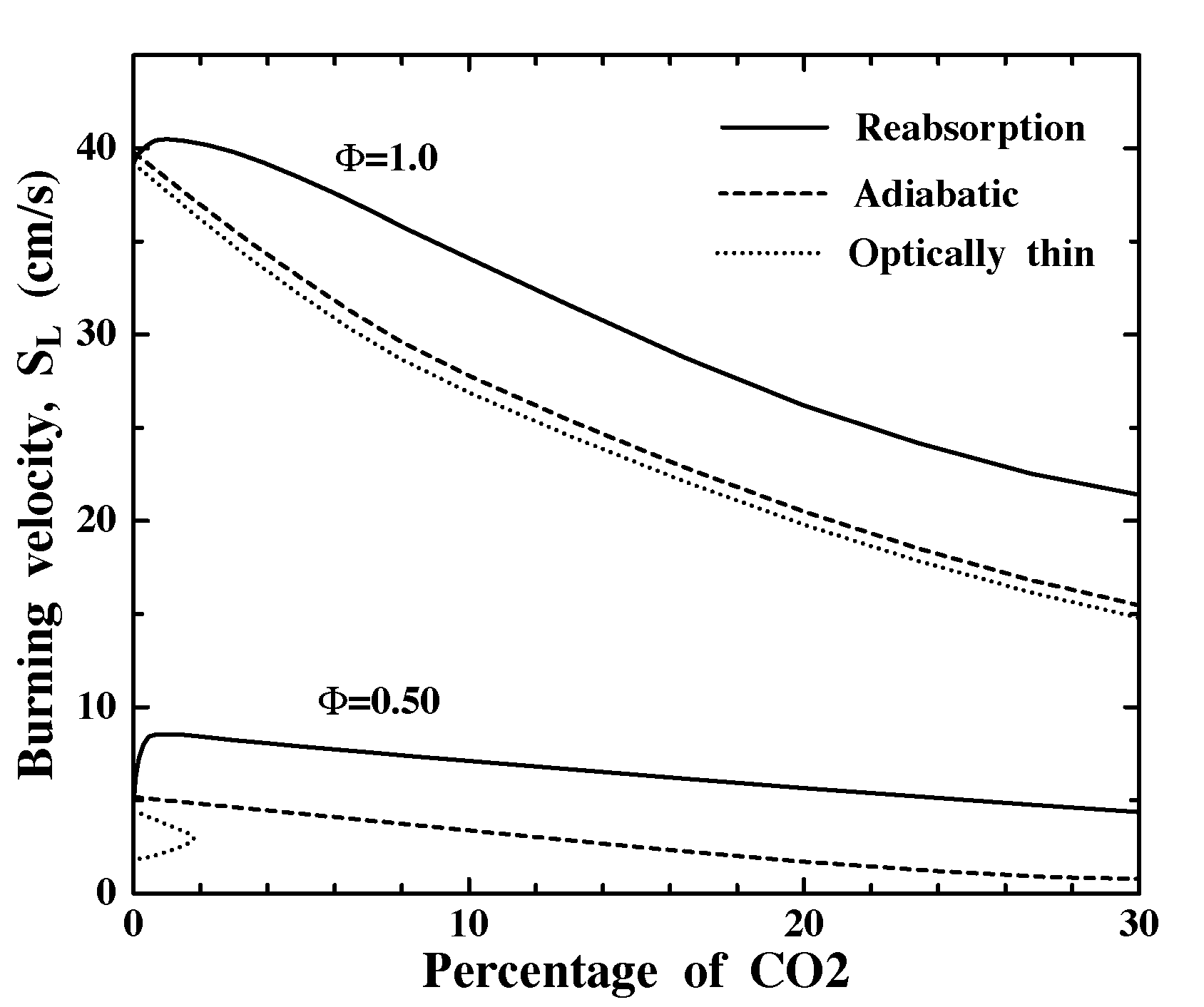
Figure 5. Effect of substitution of CO2 for N2 on burning velocities under adiabatic conditions, with optically-thin radiative losses, and with a radiative model including reabsorption effects.
Figure 6a shows that for optically-thin conditions, CO2 substitution increases Fo and SL,lim, because the additional radiating CO2 increases QR. With reabsorption, small amounts of CO2 substitution actually decrease Fo and SL,lim due to greatly reduced QR, whereas larger amounts increase Fo slightly due to reduced Tad. Figure 6b shows that for optically-thin conditions SL,lim/SL,ad is always close to the theoretical prediction [6,7] e-1/2, whereas with reabsorption SL,lim/SL,ad can be greater than 20.
|
| (a) Equivalence ratio (Fo), burning velocity (SL,lim) and peak flame temperature (T*) |
|
| (b) Ratio of SL,lim to the burning velocity of an adiabatic flame in the same mixture (SL,ad). |
Figure 6. Effect of substitution of CO2 for N2 on flammability limit properties with optically-thin radiative losses and with a radiative model including reabsorption effects
Figure 7 shows comparisons of our computed effects of reabsorption on SL to the theoretical prediction [12] SL/SL,adln(SL/SL,ad)=B for gray gases. The theory requires that (T*-Tad)/Tad be a small, O(1/b) quantity, which is justified for our conditions (Fig. 2b). Agreement is poor because the computation allows substantial net spectral heat loss (Fig. 3b) which is not considered by the theory. Agreement is improved with H2O and CO radiation suppressed (mechanism I eliminated) and still better with temperature broadening of k(w) also suppressed (mechanism II eliminated) so that the flame is practically adiabatic. Still, SL/SL,ad is much lower than theoretical predictions because the theory assumes graybody radiation, whereas gases radiate only in certain spectral bands and thus accelerate SL less than graybody radiators would. When gray-gas conditions are applied (k(w)=constant=26 m-1=LP-1), the agreement is more satisfactory, though calculated results are now above theoretical predictions, probably because the theory assumes constant thermodynamic and transport properties and single-step chemistry. Thus, our model is believed to capture the essential elements of flame propagation with graybody reabsorption plus the nuances of spectrally radiating gases.
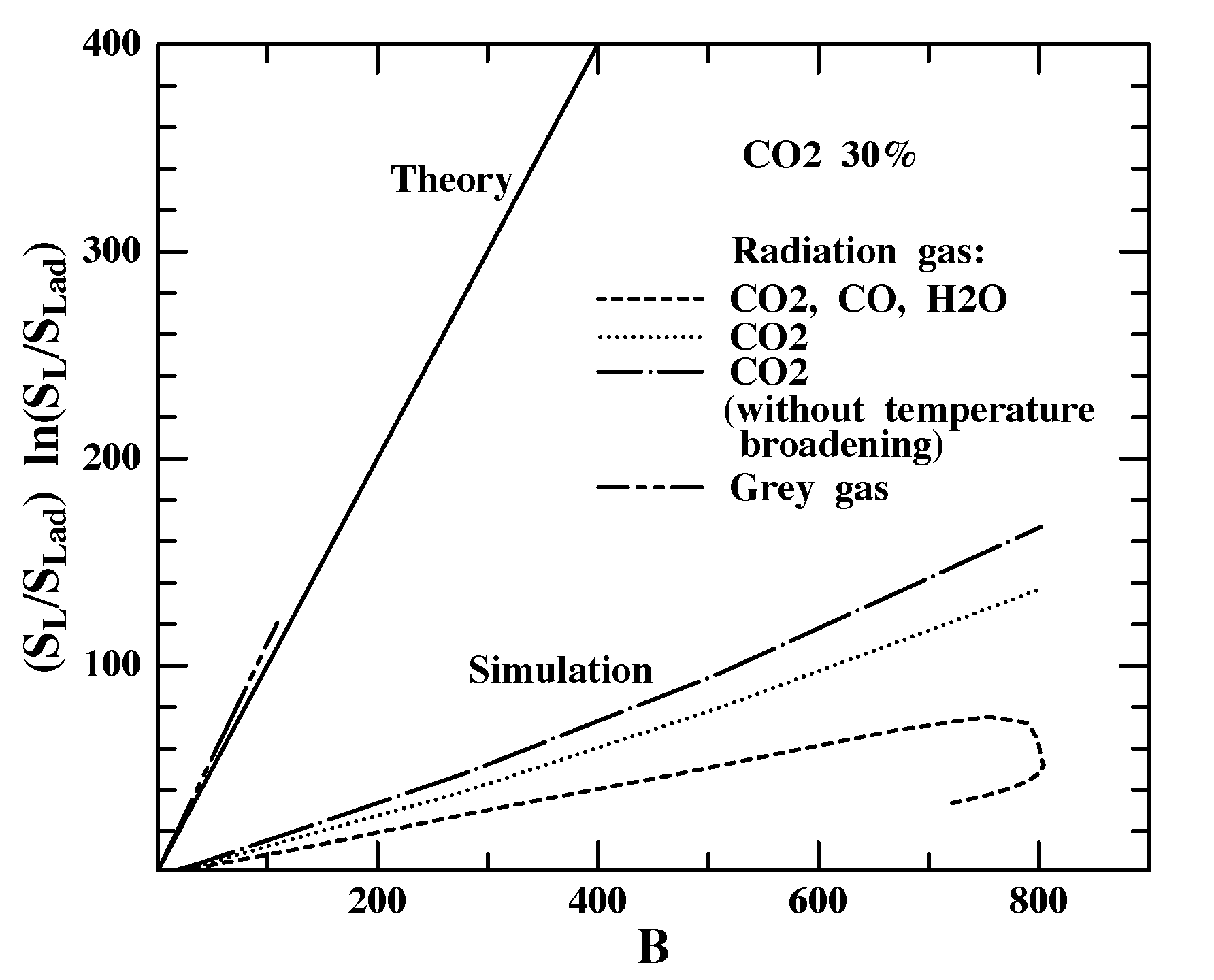
Figure 7. Comparison of theoretical predictions [12] of reabsorption effects on SL to numerical results with all radiation included, with CO2 radiation only, with CO2 radiation only with the temperature broadening of the absorption spectrum artificially suppressed, and with k(w)=constant=26 m-1 to simulate a gray gas.
Comparison with experiment
For CH4-air flames (Fig. 2a), comparison between computation and microgravity experiments in spherically expanding flames [20,21] and tubes [22] and earth-gravity experiments specially designed for low SL [23] is more favorable without reabsorption because optically-thin conditions applied to these experiments. The discrepancy between computation and experiment is significant even though the chemistry and transport models employed predict SL away from the limits quite well [24]. There is other evidence that different chemical models capable of predicting burning velocities of near-stoichiometric flames yield varying predictions of near-limit properties [25].
The only relevant SL data that may exhibit optically-thick conditions are microgravity spherically expanding flame experiments [9,26] in (CH4+4O2)-CO2 mixtures and counterflow twin-flame experiments [27] in CH4-(0.21O2+0.79CO2) mixtures (g=0.79). Neither configuration corresponds to our planar flames, but comparisons are nonetheless considered useful. To compare with [9,26], we chose L1=L2=6 cm, which corresponds to a flame radius half the vessel radius. By this radius SL was steady, yet the pressure rise in the constant-volume vessel was small (<10%). To compare with [27], we chose L1=L2=0.35 cm, which corresponds to twin flames located midway between the nozzle exits and stagnation plane for 1.4 cm nozzle separation. For both experiments, ambient values of LP are about 5.4 cm, but even for L1=L2=0.35 cm, some reabsorption is anticipated (Fig. 3a).
For the configuration of [9,26], the optically-thin model clearly over-predicts the limit fuel concentration (by 13%) and SL,lim (by 350%), thus reabsorption extends this limit. With reabsorption, SL,lim is predicted well, indicating that the net loss is correctly predicted, but the limit fuel concentration is underpredicted (by 16%), perhaps because in spherical geometry the radiative flux divergence causes less radiative preheating than would occur in planar geometry. For the configuration of [27], no numerical solutions could be obtained for adiabatic or optically-thin conditions with L1=L2=0.35 cm; this might explain why in [27] numerical predictions of SL could not be obtained. In [27] results were extrapolated to zero strain to estimate the planar SL. While the accuracy of this method for reabsorbing conditions has not been established, with reabsorption the computed and experimental values of SL agree moderately well (Fig. 8). Therefore, even for these small-scale flames, reabsorption effects may be important.
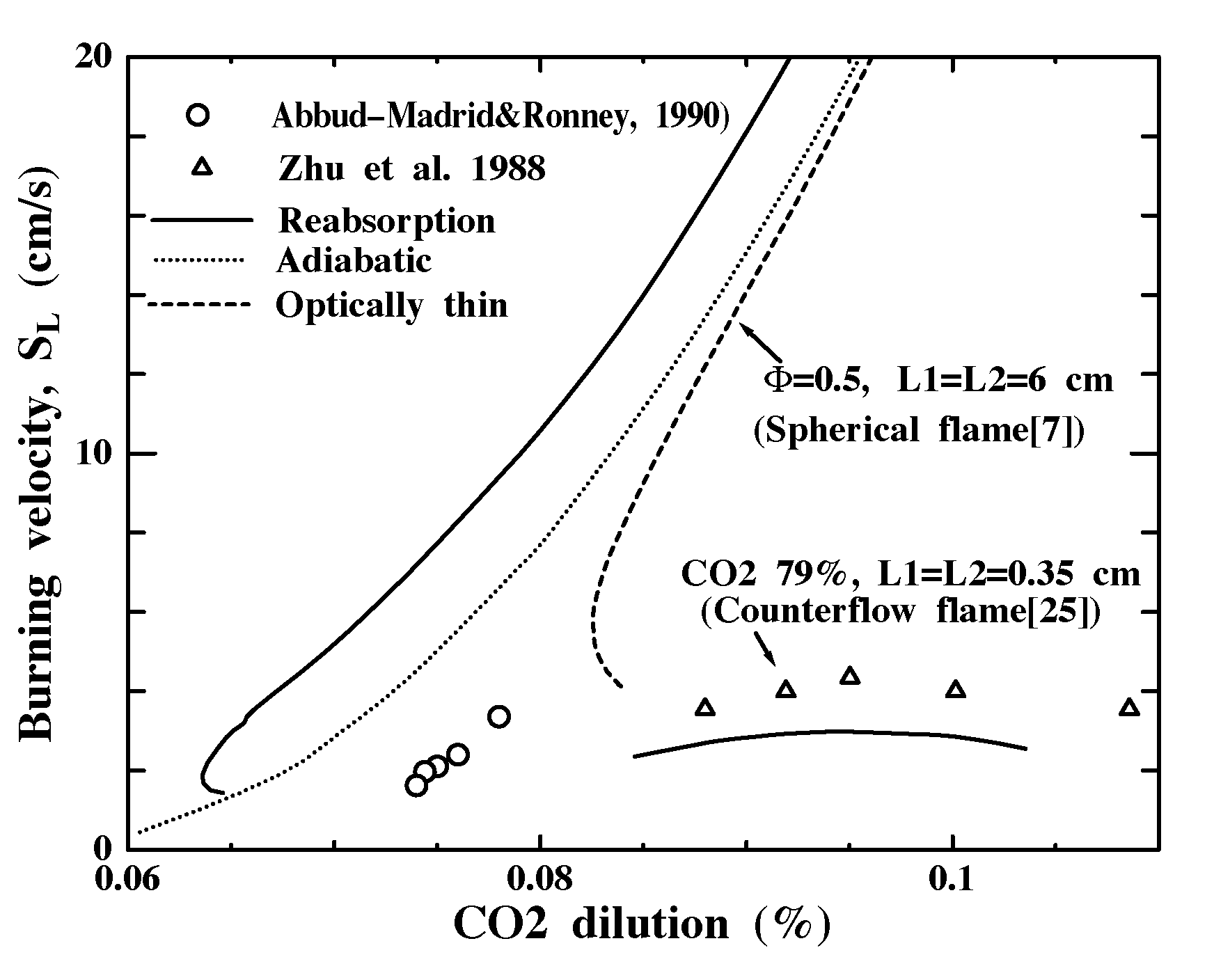
Figure 8. Comparison of numerical predictions of SL with experiments on microgravity spherically expanding flames in (CH4+4O2)-CO2 mixtures [9] and counterflow twin-flame experiments in CH4-air mixtures with g=0.79 (all N2 replaced by CO2) [27].
Conclusions
The effects of radiation on premixed-gas flames were studied using a detailed emission-absorption model for H2O, CO2 and CO. It was found that while reabsorption can increase burning velocities and extend flammability limits considerably, fundamental limits independent of the system dimensions exist due to the nature of gas radiation, specifically (I) differences between the spectral characteristics of reactants and products and (II) temperature broadening of the emission/absorption spectra. The results agree well qualitatively and in some cases quantitatively with theory and experiments.
In future work we will examine stationary "flame balls" since modeling of recent space experiments [25] suggests dominant reabsorption effects in some cases. The spherically expanding flame configuration will be studied to compare with the microgravity experiments cited above [9,26]. The effects of elevated pressures will be examined because of its relevance to IC engine and gas turbine flames. Collisional broadening of the absorption spectrum will likely be important in these cases. Finally, the effects of exhaust-gas or flue-gas recirculation will be examined via computations at elevated temperatures with CO2 and H2O addition.
Acknowledgments
PDR acknowledges support by NASA-Lewis grant NAG3-1523. Dr. Fengshan Liu (National Research Council, Canada) contributed to building the computational code.
References
1. Clavin, P., Prog. Energy Comb. Sci. 11:1-59 (1985).
2. Williams, F.A., Combustion Theory, 2nd ed., Benjamin-Cummins, 1985.
3. Jarosinsky, J., Strehlow, R.A., Azarbarzin, A., Nineteenth Symposium (International) on Combustion, Combustion Institute, Pittsburgh, 1982, p. 1549-1557.
4. Buckmaster, J.D., Mikolaitis, D., Combust. Flame 45, 109-119 (1982).
5. Jarosinsky, J., Combust. Flame 50:167-175 (1983).
6. Buckmaster, J.D., Combust. Flame 26:151-162 (1976).
7. Joulin, G., Clavin, P., Acta Astronautica 3:223-240 (1976).
8. Ronney, P.D., Twenty-Second Symposium (International) on Combustion, Combustion Institute, Pittsburgh, 1988, pp. 1615-1623.
9. Abbud-Madrid, A., Ronney, P.D., Twenty-Third Symposium (International) on Combustion, Combustion Institute, Pittsburgh, 1990, pp. 423-431.
10. Lakshmisha, K.N., Paul, P.J., Mukunda, H.S., Twenty-Third Symposium (International) on Combustion, Combustion Institute, 1990, pp. 433-440.
11. Law, C.K., Egolfopoulos, F.N., Twenty-Fifth Symposium (International) on Combustion, Combustion Institute, 1994, pp. 137-144.
12. Joulin, G., Deshaies, B., Combust. Sci. Tech. 47:299-315 (1986)
13. Abbud-Madrid, A., Ronney, P.D., AIAA Journal 31:2179-2181 (1993).
14. Kee, R.J., Dixon-Lewis, G., Warnatz, J., Coltrin, M.E., Miller, J.A., Sandia Report SAND86-8246, 1986.
15. Giovangigli, V., Smooke, M.D., Combust. Sci. Tech. 53:23-49 (1987).
16. Ju, Y., Guo, H., Maruta, K., Liu, F., J. Fluid Mech. 342:315-334 (1997).
17. Malkmus, W., J. Opt. Soc. Am. 57:323-329 (1967).
18. Soufinani, A., Taine, J., Int. J. Heat Mass Trans. 40:987-991 (1997).
19. Liu. F., Gulder, O.L., Smallwood, G.J., Ju, Y., Int. J. Heat Mass Trans. 41, 2227-2236 (1998).
20. Ronney, P.D., Wachman, H.Y., Combust. Flame 62:107-119 (1985).
21. Strehlow, R.A., Reuss, D.L., Progress in Aeronautics and Astronautics, Vol. 73, AIAA, New York, 1981, pp. 61-89.
22. Okajima, S., Iinuma, K., Kumagai, S., Twentieth Symposium (International) on Combustion, Combustion Institute, Pittsburgh, 1984, pp. 1951-1958.
23. Badami, G.N., Edgerton, A.E., Proc. Roy. Soc. (London) A228:297-322 (1955).
24. Egolfopoulos, F.N., Cho, P., Law, C.K., Combust. Flame 76:375-391 (1989).
25. Wu, M.S., Liu, J.B., Ronney, P.D., Twenty-Seventh Symposium (International) on Combustion, Combustion Institute, Pittsburgh, 1998, pp. 2543-2550.
26. Abbud-Madrid, A., M.S. Thesis, Princeton University, 1990.
27. Zhu, D.L. Egolfopolous, F.N., Law, C.K., Twenty-Second Symposium (International) on Combustion, Combustion Institute, Pittsburgh, 1988, pp. 1537-1545.