Dynamics of self-propagating
fronts of motile bacteria
Alison Kraigsley and Paul D. Ronney
Department
of Aerospace and Mechanical Engineering
University
of Southern California, Los Angeles, CA 90089-1453
Steven E. Finkel
Department
of Biological Sciences
University
of Southern California, Los Angeles, CA 90089-1340
Abstract
While much
is known about self-propagating reaction-diffusion fronts that occur in many
chemically reacting systems such as flames, polymerization processes and some
aqueous reactions, this vast knowledge base has not previously been
systematically applied to biological systems such as spreading motile
bacteria. The goals of this work are (1)
to determine if such knowledge can be applied to biological systems and (2) if
so, obtain a more quantitative and predictive understanding of biological
systems that exhibit self-propagating fronts.
The analogy between spreading motile bacteria and other self-propagating
fronts will be pursued with respect to the dynamical properties of such fronts. Initial experiments using the E. coli
bacterium do indeed show behavior analogous to reaction-diffusion systems. We are attempting to conduct a comprehensive
study of dynamical properties including propagation rates, front curvature
effects, quenching limits, stability limits, buoyancy effects, effective
diffusion coefficients and reproduction time scale. This information will be used as inputs to
existing analytical/numerical models of reaction-diffusion fronts and the
validity of the proposed analogies determined.
The differences between conventional reaction-diffusion systems and
microbiological systems will also be evaluated.
One key difference is that the bacteria evolve and respond to stress, a
factor that will be studied by repeating the above testing with bacteria that
have survived near-quenching conditions.
These data will then be used to obtain a better understanding of the
survivability and adaptation of bacteria under adverse conditions.
Introduction
Self-propagating
reaction fronts occur in many chemical and physical systems including flames,
free-radical initiated polymerization processes and some aqueous
reactions. All of these systems are
characterized by two key features: a reactive medium (for example a fuel-air
mixture in the case of flames) and an autocatalyst
that is a product of the reaction which also accelerates the reaction (for
example thermal energy in the case of flames).
Self-propagation occurs when the autocatalyst
diffuses into the reactive medium, initiating reaction and creating more autocatalyst. This
enables reaction-diffusion fronts to propagate at steady rates far from
any initiation site.
Two
of the key characteristics of self-propagating reaction-diffusion fronts are
the propagation rate (s) and the quenching limit. The propagation rate is the speed at which
the front advances into the reactive medium, which generally depends on the
overall reaction time scale (t) and the diffusion coefficient (D) of the autocatalyst
according to the relation s ≈ (D/t)1/2. t in turn depends on the concentration and activity of
the reactants. The quenching limit is
the minimum or maximum value of some parameter (for example, minimum reactant
concentration or channel width) for which a steadily propagating front can
exist. The coupling that occurs between
chemical reactions and diffusive and convective transport in flames [[1]], polymerization fronts [[2]]
and aqueous reactions [[3]]
is well understood quantitatively.
Surprisingly,
the analogous line of inquiry has not been applied to microbiological systems,
even though the very first modeling of reactive-diffusive fronts, leading to
the relation s ≈ (D/t)1/2, was conducted in 1937 in the context of the spread of
infectious diseases (see [[4]]). The purpose of our investigation is to assess
the feasibility of doing so and from this develop a more quantitative
understanding of such microbiological systems.
Most microbiological studies focus on individual bacterium and counting
the behavior of individuals. In this
study we apply thermodynamic laws and study the aggregate behavior of a large
number of individuals. The test case we
choose to focus on for this study is the very common and widely studied Escherichia
coli bacterium, a motile bacterium that (like many others) swims using its
tentacles or flagella in its nutrient media while frequently changing
direction to seek regions of higher nutrient concentration. Specifically the bacterium has two modes of
behavior: “run” mode in which its flagella rotate to propel it in a more or
less straight line, and “tumble” mode where the flagella cause it change
orientation with little net motion [[5]].
The resulting motion is somewhat analogous to the random walk of
molecules that leads to classical Fickian diffusion
(although the mechanism is entirely different, since, unlike molecules the
bacterium motion is not related to elastic collisions between bacterium). Also, in a favorable nutrient gradient, the
bacterium runs more than it tumbles, resulting in higher D, whereas in
unfavorable gradients, it tumbles more, allowing it to seek out new directions
and resulting in lower D; this also leads to a biased random walk that favors
migration to regions of increased nutrient levels.
These
characteristics of motile bacteria can be exploited to model their behavior as
reaction-diffusion fronts. The propagation speed (s) of E. coli we
measured (see Preliminary Results section) in a 0.3% agar medium is about 4.5
mm/hr. The reproduction time scale (t) of E. coli is about 20
min. Since the propagation speed s ≈ (D/t)1/2, D ≈
s2t, thus D ≈ 1.5 x 10-5 cm2/sec. This value is consistent with the value
expected based on the kinetic theory of molecules which shows that D is
proportional to a particle speed (c) multiplied by the particle mean free path
(l), i.e., in the case of molecules the distance
the particles move before colliding with each other, or, in the case of motile
bacteria, changing direction. l can be
estimated as c multiplied by the time (t) the bacteria swim without changing
direction. For E. coli, an
average swimming speed of 21 µm/s, with 21 changes in direction per 30 seconds
has been measured. This implies ≈
1.4 s and l ≈ 3.0 x 10-3
cm and, thus the effective diffusivity D ≈ 6.3 x 10-6 cm2/s,
which is of the same order of magnitude as the value of D inferred from D ≈ s2t.
We
conclude that it is reasonable to characterize the spread of motile bacteria as
reaction-diffusion fronts. Many
microbiological studies measure the response of the system to a gradient in
temperature or nutrients that is imposed on the system; we intend to show that
the bacteria can generate their own gradients and thus can be self-propagating. Table 1 shows the proposed analogy between
flames (a typical reaction-diffusion front) and microbiological systems.
|
Flame or molecular property |
Microbiological equivalent |
|
Temperature |
Concentration of bacteria |
|
Fuel |
Nutrients |
|
Heat diffusivity ≈ cl |
Diffusivity of bacteria |
|
Fuel diffusivity |
Diffusivity of nutrient |
|
Sound speed (c) |
Swimming speed of bacterium in
"run" mode |
|
Mean free path (l) |
c multipled
by average time to switch from run mode to tumble mode and back |
|
Reaction timescale (t) |
Reproduction time |
|
Heat loss |
Death (of individual bacterium) |
|
Quenching |
Death (of all bacteria) |
|
Table 1. Proposed analogy between flames and
microbiological fronts |
|
A complicating factor in flames as well
as the motile bacteria is that the effective diffusion coefficient changes with
product concentration. In the case of
flames, the production of products leads to higher temperature that increases D
in nearly all cases. In the case of
motile bacteria, it is well known that the bacteria spend less time in the
"run" mode and more in the "tumble" mode when the nutrient
concentration is high (why look around when the grass is already green?) This means that the mean free path l will be
lower and thus the effective diffusivity will be lower when the nutrient
concentration is high. In the case of a
propagating front, the few bacteria at the leading edge of the front see high
nutrient concentrations and thus have low D.
The higher concentrations of bacteria (the "product" of
reaction) at the trailing edge of front will exist in a medium with lower
nutrient concentration and thus will "run" more and
"tumble" less, increasing l and thus D will increase. Thus the analogy with flames is reasonably
broad.
Preliminary results
The above
discussion encouraged us to conduct preliminary experiments to test the
viability of our propositions. These
experiments were conducted at 37˚C in standard petri plates using a water-based
nutrient medium consisting of (unless otherwise noted) 1% NaCl,
1% tryptone, 0.5% yeast and 0.1% agar. The agar increases the viscosity of the
medium and essentially prevents any bulk motion. The medium was inoculated with bacteria at a
point (usually at the center of the dish) and the resulting advance (if any) of
the bacteria front was observed visually.
Several strains of E. coli were tested. After an initial transient, all exhibited a
linear increase of front radius with time.
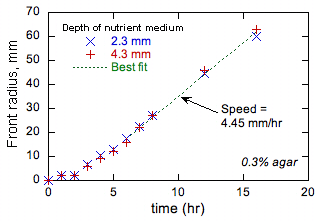
An example is shown in Fig. 1.
Figure 1
shows that the front advances more slowly initially when the front radius is
small and front curvature high. All
other tests showed this same trend. This
behavior is observed in chemical fronts in which the autocatalytic product has
a lower diffusivity than that of the reactant (i.e., in the case of
flames, a high thermal diffusivity and a low fuel diffusivity) and the reasons
are well understood [[6]]. While the diffusivity of the tryptone nutrient is unknown, by analogy with similar
molecules a value of 10-7 cm2/s can be estimated, which
is lower than the apparent diffusivity of E. coli as estimated above.
Consequently, the behavior shown in Fig. 1 is consistent with the
reaction-diffusion model of front propagation. Furthermore, flame theory shows
that if the ratio of product to reactant diffusivities is too different from
the value 1, either higher or lower, various types of front instabilities may
result. Pattern formation in microbiological systems is well known [[7]],
but reaction-diffusion theory has not been used to quantify and predict such
patterns. We will investigate such
instabilities by varying the medium diffusivity through the agar
concentration. Moreover, we suspect that
this choice of the run-tumble timing of E. coli is not accidental
because it affects D; if D is too low or too high, instabilities result that
may be unfavorable for survival. We will
pursue this notion by examining the effect of agar concentration on the speed
and run-tumble timing of the bacteria under a microscope and determine if the
bacterium adapts (either on the fly, or by evolutionary processes) its speed
and run-tumble timing to modify its effective D to maintain stable fronts.
|
|
|
Figure 1. Example experimental data on bacterial
front radii as a function of time. |
|
|
|
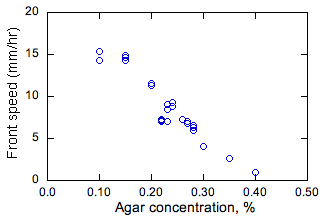
Figure 2. Measured effect
of agar and solution depth on steady propagation speeds of bacterial fronts. |
The effect
of agar concentration and the depth of the nutrient medium on the steady values
of the propagation rate s is shown in Fig. 2.
At 0.5% or greater agar concentration (not shown), the medium was
essentially solid and the bacteria spread only on the surface of the medium,
not in the bulk. Diffusion-like behavior
of the bacteria is unlikely in this case since they cannot swim. At 0.4% and lower agar concentration, the
bacteria spread through the medium. The
highest propagation rates (s) were observed at the lowest agar concentrations
(and thus lowest viscosity of the medium).
This is expected since at lower viscosity, the bacterium can swim faster
and thus should have higher effective D, leading to higher s (since s is
proportional to D1/2 as discussed above).
The depth of the solution was found to
have almost no effect on s. By taking
cross-sections of the medium after partial propagation of the front, it was
found that the fronts are mostly uniform in the vertical dimension. Thus buoyancy flow is not affecting these
fronts, otherwise an effect of the solution depth on s, or non-uniformity in
the vertical direction, would be expected.
Since the tests were conducted in air, these observations also indicate
that oxygen diffusion into the medium is not significant, otherwise growth near
the surface of the nutrient solution would be different from that below the
surface. This last result shows that the
bacteria are growing anaerobically.
To
determine whether "quenching" limits exist in bacterial fronts, an
experiment was conducted in which the bacterial fronts attempted to propagate
through narrow and wide channels with antibiotic walls. Since antibiotics remove the autocatalytic
product (the bacteria), the effect of the walls is analogous to heat losses to
cold walls in flames. For front
propagation in narrow channels, it is well known that a quenching limit occurs
due to heat losses to the channel walls when the Peclet number Pe = sw/D, where w is the channel
width and D is the diffusivity, is less than a critical value. Thus, in the presence of heat losses, fronts
can propagate through wide channels (high Pe) but not
narrow channels (low Pe). Figure 3 shows that fronts can propagate
through the wide channel but not the narrow channel, indicating a quenching
limit. The applicability of the
quenching relationship Pe = sW/D
= constant at the limit will be tested in this work.
The effect of tryptone
nutrient concentration was also tested; it was found that at half the nominal
value no spread would occur, whereas s was almost unchanged by doubling the tryptone concentration from its nominal value. This may indicate a quenching limit even in
the absence of antibiotic walls.
Analogous behavior occurs in flames due to radiative heat losses when
the fuel concentration is too low. We
will investigate this wall-free limit and attempt to determine the loss
mechanism responsible for suppressing front propagation at low nutrient levels.
Titering of the medium to obtain bacteria counts
consistently showed a significant peak in the bacteria concentration at the
leading front, followed by a major drop behind the front and, for later times,
a second peak far behind the first one.
This is consistent with the images shown in Fig. 3. In future work we will use titering analysis to determine if the front thickness ≈ D/s
as predicted theoretically. Based on
visual inspection of Fig. 3 the front thickness is about 1 mm, which is close
to the prediction D/s = (1.5 x 10-3 mm2/sec)/(4.5 mm/hr) = 1.2 mm.
Results with a wild strain of bacteria showed a slightly faster initial
transient and a shorter time and distance to reach steady a steady propagation rate
as compared to genetically marked strains.
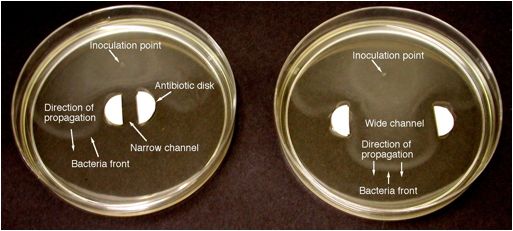
Figure 3.
Photographs of fronts of motile E. coli bacteria propagating through
narrow (6 mm, left) and wide (35 mm, right) channels with Kanamycin antibiotic
side walls (100 microliters of Kanamycin per side), taken 6.5 hours after
inoculation. Both cases: 2086 wild strain of E. coli, 0.1% agar,
standard nutrient medium.
Current research program
Based
on the apparent success of the reaction-diffusion model in describing in these
preliminary experimental results, we are pursuing the following research
program:
- Determine the propagation rates
of E. coli fronts as a function of nutrient concentration, medium
motility (through changing the agar concentration), ambient temperature, ambient
oxygen concentration (aerobic vs. anaerobic environment), and the
thickness of the layer of nutrient medium.
These tests will be performed in the same manner as the preliminary
experiments described above.
Additionally, to improve visualization of the fronts, we will use E.
coli specific fluorescent dyes from Molecular Probes, Inc (Eugene, OR). to improve visualization of the
fronts. An ultraviolet light
source (purchased) or Ar-ion laser will be used
to excite the fluorescent dyes.
- Determine D based on the
relation D ≈ s2t and
compare with that expected based on the relation D = c2t, where c is the measured
(using video microscopy) speed (c) and t mean time to change
direction. Standard video is
adequate since the run-tumble time scale is typically 1 sec and the video
framing rate is 30 per sec.
- Determine the quenching limits
and limit Peclet numbers by allowing the fronts to propagate through
channels of varying width (w) having antibiotic walls (Kanamycin or
similar) and determine if Pe is constant at the
limit, i.e., is the propagation rate (s) at the limit proportional
to 1/w?
- Determine the quenching limit
in the absence of walls (by decreasing nutrient concentration, for varying
agar concentrations) and ascertain the loss mechanism (i.e. cell
death mechanism) responsible for this limit.
- Determine the stability limits
as a function of the ratio of product (bacterium) to reactant (nutrient)
diffusivity by varying the agar concentration in the nutrient medium and
nutrient concentration. The fluorescent
dyes will facilitate imaging of non-uniform fronts and pattern formation.
- Determine if a buoyancy effect
on front propagation exists. Since E.
coli bacteria have a density slightly different from water, at low
viscosity a buoyancy effect will occur.
Most investigators use a high-viscosity agar medium to prevent any
fluid flow, but many real E. coli environments have water-like
viscosity. Buoyancy effects will be
examined by testing front propagation in agar-free media in a vertical
parallel plate apparatus (called a "Hele-Shaw"
cell in fluid mechanics literature) and the front pattern and propagation
rate will be observed.
- Model these results using our
existing analytical/numerical models of reaction-diffusion fronts.
Of course,
there are also some differences between conventional reaction-diffusion systems
and microbiological systems. One key
difference is that the bacteria evolve and respond to stress, a factor that
will be studied by repeating the above testing with "experienced"
bacteria that have survived near-quenching conditions. Another difference, as discussed above, is
the biased diffusion properties. This bias can be modeled using a nonlinear
diffusion relation to replace Fick's Law.
Practical
importance
This
work is a study of the dynamics of a new class of propagating fronts involving
motile bacteria. The study of front
dynamics has many applications as discussed above. These studies, however, are of particular
interest to microbiologists because it relates to the mechanisms of long-term
survival and evolution used by bacteria.
One of the primary factors influencing the rates of evolutionary change
in these bacterial systems are the levels of environmental stress, as well as
the transition from one environment to another.
The culture systems we are developing represent new environments in
which these questions of evolution and survival have not been addressed. This work provides the first attempt, to our
knowledge, to characterize these effects biophysically.
The
study of E. coli growing under anaerobic conditions is of particular
interest. When E. coli (and all
other enteric bacteria) grow in association with the human digestive tract,
they grow under anaerobic conditions. We
wish to begin to study bacterial stress responses in the absence of oxygen to
further expand our general understanding of how this bacterium adapts to life
in a wide variety of environmental niches.
For example, it is not currently known if the mechanisms of DNA damage
repair and mutation that Prof. Finkel has been studying (and which he has shown
to be important for adaptation to novel environments) function under anaerobic
conditions. These studies will bridge
the gap from basic research into more medically relevant areas.
Not
proficient in English? Try the Swedish version. Or the Russian version. Or the
Tatar version. Or the Romanian version. Or the Estonian version.
Or the Czech version.
Or the Turkish version. Or the Polish version. Or the Bosnian version.